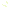|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
FRACTION GAMES - VISIONS AND REVISIONS
. |
|
|
|
|
|
|
|
|
|
|
by Albert B.Bennett, Jr. and Peter Schiot |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Time for you and time for me, And time yet for a hundred indecisions, And for a hundred visions and revisions, Before the taking of a toast and tea. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
from The Love Song of J. Alfred Prufrock by T. S. Eliot |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Playing games has long been recognized as a method of teaching mathematical concepts and skills to obtain student involvement and enthusiasm. However, the potential for motivation and learning when students revise games or create their own games is not as well known. In the article, "Mathematics Students Have a Right to Write," from the May 1983 issue of The Arithmetic Teacher, Joan Shaw notes that devising games requires the three essential elements of writing: prewriting (inventing and creating); writing (stating rules); and rewriting (trying the game and making adjustments). The purpose of the following article is to describe the activities of a fifth grade class which was exposed to the combination of reading-writing process and mathematical games.
As part of their instruction in the reading-writing process, the students learned to assume responsibility and control of their own learning by continually questioning and evaluating everything they read and write. They were encouraged to develop critical judgment and made to feel their ideas and views were worthwhile. In their mathematics instruction the students were taught published games for learning about fractions.*
An unexpected outcome was the spontaneous desire of many of the students to revise the given games or to create their own games. By revising published games, and in most cases producing more sophisticated games, the students had a means of measuring their accomplishments. The student became the author and inventor, teaching his or her own rules to other students and adults. As owner of the game, the student became responsible for its improvement, playing and revising the game many times while sharing and exchanging strategies and knowledge of fractions. At the beginning of the school year each student was issued a deck of fraction bars. |
|
|
|
These bars represent halves, thirds, fourths, sixths, and twelfths. The bars can be described before fractions are introduced by stating the total number of parts and the number of shaded parts. For example, one of the bars shown here has 12 parts and 5 parts are shaded; or, 5 out of 12 parts are shaded. Counting the zero-bars (no parts shaded) up to the whole-bars (all parts shaded) there are 32 different bars. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The teacher introduced the fraction games by showing each game to one or two students. The students were then responsible for teaching the game to their classmates. A grid with the names of the students and games showed who was responsible for each game and which students had played the game. As examples, Emily (EW) was responsible for teaching Double or Nothing as she taught this game to 23 students; and Dan and Amy were responsible for teaching Fraction Bingo. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
In addition to spending time on computation and problem solving during the first two months, the students played games with fraction bars. During this time they did not use fraction numerals or terminology. As examples, a 3/4 bar was described as "three parts out of four" and 1/6 as "one part out of six."
After the games had been played a few times some students began to change the rules to improve the games or make them more challenging. Here is one of the games which was taught by the teacher. This game provides readiness for addition. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
At first the students played this game by placing the shaded amounts of the bars end to end to determine the total shaded amount.
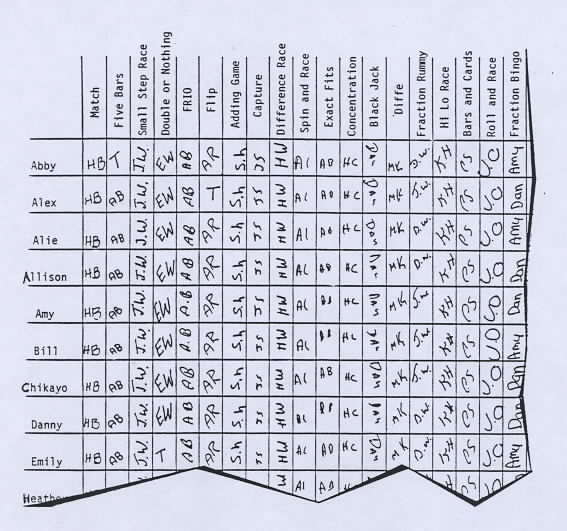
Gradually, this became unnecessary as the students became familiar with the bars. Mike and Alex revised Fraction Bars Black Jack (see illustration) by requiring that three arbitrary fraction bars be placed face up at the beginning of each round. The total shaded amount of these bars became the "target" for the round. They called their game Super Black Jack. In one round the following three bars were selected. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Mike explained that the red bar can be combined with the green bar to form one whole bar with one part out of six left over. This can be put with the orange bar to give nine parts out of twelve. So for this round each player tried to get as close as possible to one whole bar and nine parts out of twelve. Alex won the round with the following four bars. He matched his red bar with the one on the board and put the leftover part of the red bar with his yellow bar to equal the shaded amount of the green bar. Then since one part out of four equals three parts out of twelve, he held with one whole bar and five parts out of twelve. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Every fraction bar has a corresponding playing card of the same color. When fraction numerals were introduced each student was supplied with a deck of fraction playing cards. The students usually combined their bars or cards to obtain a deck of 64 bars or 64 cards for a game. To help in sorting, the backs of each student's bars and cards were labeled with his or her initials.
There have been several memorable stories about students learning with the fraction bars. For example, shortly after the introduction of fraction numerals, one parent wanted to know if her son was learning about fractions by using the bars. The teacher asked the boy to deal out five fraction bars and find the smallest common denominator of the fractions. The boy gave both the smallest common denominator and the sum of the five fractions, while the parent was still trying to find the smallest common denominator. Needless to say, the parent went away satisfied.
One game which helps to provide a transition between the concrete (Fraction Bars) and abstract (fraction numerals) is called Bars and Cards. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Over a period of several weeks, Mariana and Alexandra revised this game many times. They called their version Super Bars and Cards. Instead of placing 10 bars face up, each player is dealt five bars to be used only by that player. As in the original game, whenever a bar is won by a player another bar is put in its place. They created a discard pile of unused cards, which are placed face up. A player can now select a card from the deck or the discard pile. They also allowed equality and sums. That is, a player can win a bar if the fraction from the playing card equals the fraction from the bar; or, he or she can win several bars if the sum of the fractions for the bars equals the fraction on the card. If a player uses a card from the discard pile to win one or more bars, he or she can continue playing by taking another card from either the deck or the discard pile. But if the player selects a card from the deck, he or she cannot take another card on that turn. When all the cards in the deck have been used, the discard pile is turned over and used as the deck. |
|
|
|
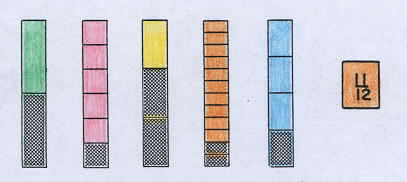
The game continues until all the bars have been won or no more plays are possible. At one time Alexandra had these bars, and turned over a playing card with 11/12. She won two bars by combining the 2/3 bar and the 1/4 bar to get 11/12. How could she have won three bars? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Many of the published games which were designed for fraction bars were changed by the students so that they could be played with both the bars and cards. The next game is described with fraction bars, and the students' version shows how fraction playing cards were brought into the game.** |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Kristan and Abby redesigned this game and called it Super Double FRIO. They allowed each player to rearrange her or his bars to obtain an increasing or decreasing sequence of fractions. However, to win the game the difference between any two adjacent fractions must be 1/12. Their game uses the bars and fraction playing cards which are both placed face down in separate decks.
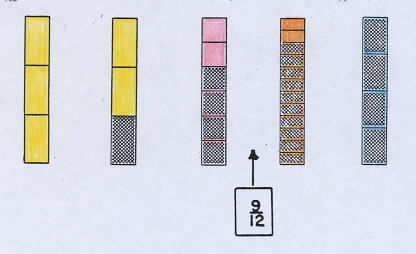
On a player's turn he or she may select a bar or card. If a bar is chosen it may be used to replace any of the player's bars, as in the original game. But if a card is chosen it may be placed to the left or right of any bar, and any one of the five bars may be removed. For example, Abby had the five bars shown below and selected a playing card with 9/12. She put the 9/12 card between the 4/6 bar and the 10/12 bar to obtain three fractions in order, and removed the 4/4 bar. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Since the bars and cards are colored (halves green, thirds yellow, fourths blue, sixths red, and twelfths orange), a player always knows the denominator of the fraction on the top bar or card in a deck. Therefore, a player's strategy may be to choose a bar rather than a card depending on the fraction that is needed. In a later revision of this game the students placed the unused bars face up in a discard pile and the unused cards face up in a discard pile. On a player's turn, he or she can select a bar or card from the two decks or two discard piles. The first player to obtain five fractions in order wins the game.
The preceding games are only a few of those which were revised or created by the students. Seth and Jason created Super Concentration when Seth was teaching Jason the Addition Game. Heather and Tosca created Super Rummy in which a player tries to obtain runs of three or more "consecutive" fractions which increase by either twelfths, sixths, fourths, thirds, or halves. Alie, Amy, Chikayo, and Jenny invented a game called Two Run. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Several students organized tournaments for some of the games. Alex and Billy set up a tournament for Number Line Racing. The Equality Race tournament which is shown below was organized and managed by Jon. In all the tournaments there was a winner's champion and loser's champion, and they competed for the class championship. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
USE OF GAMES |
|
|
|
|
The fraction games are usually played in the students' spare time, after regular assignments have been completed. The readiness period for using the bars and playing the games should not be rushed. Preferably, the games should be played over several weeks rather than during a concentrated period. When fraction numerals are introduced, they will be used by students as a convenient notation for representing ideas with which they are familiar.
The Fraction Bar games and workbook are appropriate for grades 3 through 8. Many of the readiness games (before fraction numerals) have been used in grades 1 and 2. Joyce Strong, a first grade teacher at Oyster River Elementary School, has used several of these games with her students.
The fraction games have been used with a wide range of students, from learning disabled to gifted. One of the school's most severely handicapped learning disabled students had problems in processing and memory recall. According to tests which were given in earlier grades, this student was incapable of learning about fractions. However, the student eventually played most of the Fraction Bar games and successfully completed the workbook sections on basic concepts of a fraction and equality of fractions. Even students who are capable of computing with fractions can gain an understanding of fractions from visual experiences with the bars. These students not only have algorithms for using fractions, but they will be able to provide intuitive explanations. As examples, a student might explain that 1/3 > 1/4 because when a bar is divided into 3 equal parts, the parts are bigger than when the bar is divided into 4 equal parts; or, that 1/2 = 2/4 because if both parts of a 1/2 bar are divided in half, there will be 4 parts and 2 shaded parts. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CONCLUSION |
|
|
|
|
Several advantages have been gained from the combination of mathematical games and reading-writing instruction in the fifth grade class whose activities are described above. The emphasis on critical judgment and acceptance and promotion of student ideas resulted in an unusual amount of student initiative and creativity. The variety of published games provided the initial mathematical ideas that the students could easily learn, and then use in their games. In the process of creating and revising games, the students were involved in prewriting (creating new rules), writing (stating rules), and rewriting (making final adjustments). Perhaps of equal importance are the positive attitudes, as evidenced by the students' voluntary participation in the process of creating and revising new games, and their pride in sharing these games with others. The students' rewards were the challenges of developing better games and the recognition of having done so. Not only were the students peer teachers, teaching their games to other students, but they also taught their games to the teacher, student teacher, and teacher aide. By revising and creating games the students could begin to view rules as the results of human choices, and not as something fixed or authoritative. By proposing new rules and then playing the games and refining the rules, the students experienced the excitement of developing and evaluating their own ideas. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Albert B. Bennett, Jr. is an Emeritus Professor of Mathematics at the University of New Hampshire. Peter Schiot was a fifth grade teacher at the Oyster River Elementary School in Durham, New Hampshire. For further information on fraction games, contact: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Albert B. Bennett, Jr., Department of Mathematics, University of New Hampshire, Durham, NH 03824
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
REFERENCES |
|
|
|
|
|
|
|
|
Bennett, Jr., Albert B. 2009. Fraction Bars. Fort Collins, CO: Scott Resources, Inc.
Graves, Donald H. 1983. Writing: Teachers and Children At Work. Exeter, NH: Heinemann Educational Books.
Shaw, Joan G. May 1983. "Mathematics Students Have a Right to Write." The Arithmetic Teacher, 30:16-18. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
END NOTES |
|
|
|
|
|
|
*These games are from Bennett, Jr., Albert B., Fraction Bars Teacher's Guide Grades 5-8 (Fort Collins, CO: Scott Resources, Inc. 2009)
**FRIO was first described by Rowenda Drizigacker, Arithmetic Teacher, Vol. 6, No. 4, December 1966, 436-37.
"Fraction Games - Visions and Revisions" was published in Teaching Mathematics: Strategies That Work, edited by Mark Driscoll and Jere Confrey, 1985. It is printed here by permission of the Northeast Regional Exchange. |
|
|
|