Home
Multiplication Involving Fractions
 
Materials: Deck of bars, water-base pens, and paper and pencil for each student

Fraction Times Fraction
Place a transparent bar for 1/3 on the overhead, and ask students what part of a bar they would have if they had 1/2 of this amount. Discuss comments and suggestions, and if it does not come up, illustrate the answer by splitting the shaded part into 2 equal parts and double shading one of them. This double shaded part is 1/6 of a whole bar, which can be shown by comparing it to a 1/6 bar or by splitting each of the 3 parts of the 1/3 bar into two equal parts to see that the double shaded part is 1 part out of 6. Tell students that taking 1/2 of 1/3 is multiplying the fraction 1/2 times 1/3, and write the equation 1/2 x 1/3 = 1/6.

Group Activities:

a. Select an arbitrary bar with one part shased, determine 1/2 of the shaded amount, and write the resulting product. This can be done by drawing on the bars with water-base pens or tracing a bar on paper and dividing the shaded amount into two equal parts. Discuss some of the results.

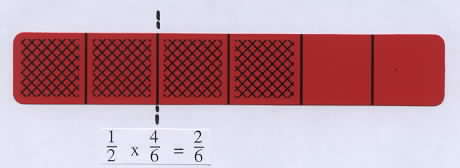
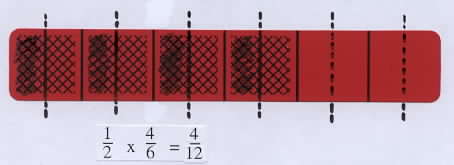
Then ask students to select any bar with an even number of shaded parts, write its fraction, and determine the fraction for half of this amount. For example, if the bar below for 4/6 is selected, one of the following methods shown might be used: take half of the shaded parts, as shown on the left below; or split one of the shaded part in half to get 1/12 and do this for all four shaded parts, as shown below on the right. Point out that this second method leads directly to the product 1/2 x 4/6 = 4/12, which illustrtes the standard algorithm for multiplying fractions:

-numerator times numerator and denominator times denominator-

Take 1/2 of the total shaded part. Take 1/2 of each shaded part.
b. Make up a word problem which requires computing 1/2 x 1/3.
Example: If sister has 1/3 of a cake and gives her brother 1/2 of it, how much will he have?
c. For further activities involving multiplication of a fraction by a fraction see shading Blank Fraction Bars, Activity Sheet #5.
 
Research Results
The National Assessment of Educational Progress has found a common student belief that multiplying produces a larger number.

We can help students overcome this belief by connecting multiplication of whole numbers to multiplication of fractions by teaching that the first number in a product tells what to do with the second number. If the first number is a whole number, it can tell us to take the second number zero times, one time, or many times (repeated addition). If the first number is a fraction less than one, then the product will be smaller than the second number because fractions less than one tell us to take part of an amount. In this case multiplication produces a smaller number.