|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Division Involving Fractions |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Materials: Deck of bars and sheets of Blank Fraction Bars for each group
|
|
 |
|
|
|
|
|
|
|
There are two major concepts of division involving whole numbers: (1) the measurement concept; and (2) the sharing concept, and these both are used in the same way for fractions. For example, one type of question for division of whole numbers is: "How many times does 3 go into 15?’ this is jokingly referred to as the "Gasinta method". The answer to such a question can be determined in various ways, but one is by subtracting off (measuring off) as many 3’s as possible from 15. Another type of question involves the idea of sharing: "If 18 markers are divided equally among 3 people, how many will each person receive?" Both of these concepts of division commonly arise in solving problems involving fractions. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fraction Divided by Fraction |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Show bars for 2/3 and 1/6 and ask how many times 1/6 "goes into" 2/3. Write the quotient under the bars. Illustrations such as this can help to show that division of fractions is closely related to division of whole numbers, that is, both involve finding how many times bigger one number is than another. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2/3 ÷ 1/6 = 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Show bars for 5/6 and 1/3 on the overhead and ask how many times 1/3 "goes into" 5/6. Ask for illustrations and discuss. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5/6 ÷ 1/3 = 2 1/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Most people will see that the quotient is greater than 2 and less than 3, but may not know what to do with the 1/6 remainder. Others may say that the quotient is 2 and 1/2 but not be able to explain why. Point out that to compute 16 ÷ 3, we determine the whole number part of the quotient, 5, and use the remainder of 1 to form the fraction 1/3, because the remainder is 1/3 of the divisor. Similarly, in dividing 5/6 by 1/3, the remainder 1/6 is half of the divisor 1/3, or we could say that the shaded amount of 1 part out of 6 is half as big as the shaded amount of 1 part out of 3. So, the quotient is 2 and 1/2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Group Activities:
a. Find bars for 1/2 and 1/6 and explain with a visual diagram why the quotient of the larger fraction divided by the smaller is 3.
b. Make up a word problem that requires computing 1/2 divided by 1/6.
Example: If there is 1/2 of a pound of butter and each batch of cookies requires 1/6 of a pound, how many batches can be made?
c. For further activities involving division of a fraction by a fraction use Blank Fraction Bars together with activity #6 Shading Blank Fraction Bars to Determine Quotients of Fractions. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fraction Divided by Whole Number |
|
|
|
|
|
|
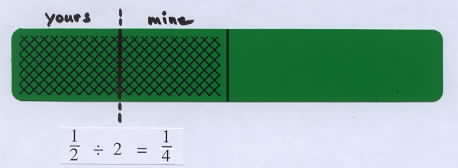
Show the bar for 1/2 and ask someone to determine what part of a whole bar they would have if you both equally shared the shaded amount. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Then divide the shaded amount in half, label each amount 1/4, and write the corresponding division equation. 1/2 ÷ 2 = 1/4. Point out that this is an example of the "sharing concept" of division. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Group Activities:
a. Select an arbitrary nonzero bar, determine the amount you would receive if the shaded amount was shared equally with another person, and compute the quotient of the fraction for the shaded amount divided by 2. Discuss some examples. One activity is to shade blank bars and split the shaded amount.
b. Make up a word problem which requires computing 1/3 divided by 4.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Whole Number Divided by Fraction |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Show bars for 1 and 1/4 and write the division equation for 1 divided by 1/4. Discuss the fact that 1/4 "fits into" 1 four times, or that 1 is four times greater than 1/4. Ask what the quotient would be if the 1/4 bar was replaced by a 1/6 bar or a 1/12 bar. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 ÷ 1/4 = 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Answers: If a 1/6 bar is used the quotient will be 6; if a 1/12 bar is used the quotient will be 12. Discuss and ask how these result can be generalized. The important idea here is that as the divisor gets smaller, the quotient gets bigger, which helps to show that division determines the relative size between two numbers. Activities such as this can help students dispel the common belief that "division makes smaller". |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Invert and Multiply: NCTM's Standards 2000, page 219, notes that students have difficulty remembering the "invert and multiply" rule for dividing with fractions. This algorithm for division of fractions is difficult for some students, but visual and meaningful examples, such as those shown above, can help refresh the memory. Students can easily visualize an example such as 1 ÷ 1/4 = 4, which shows that inverting the second number and multiplying, 1 x 4/1 = 4,produces the correct result. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Research Results from 7th NAEP Assessment |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Show the following NAEP table and discuss. The large percent of incorrect responses by both the eighth and twelfths graders is likely due in part to students’ not seeing that this problem is asking for the relative size of two numbers and that the answer can be found by division. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Equation mats can be run off for all four operations with fractions. Each of the equations for addition and subtraction have three blanks for placing fraction bars, and each of the equations for multiplication and division have two blanks for placing bars, with whole numbers printed for the multiplier and quotient. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Photo courtesy of Herb Moyer |
|
|
|
|
|