Home

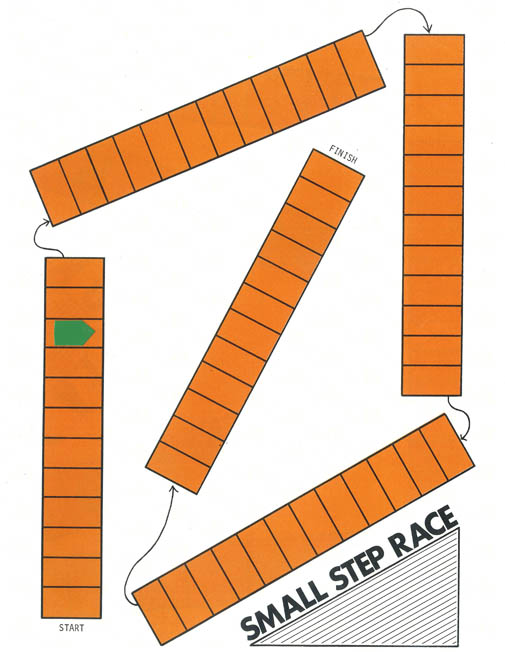
Small Step Race (equality, addition, multiplication)

Materials: Fraction Bars, Small Step mat, markers, and a die per group or pair of players

Use a Small Step mat to illustrate two or three moves by selecting bars and moving the marker according to the shaded amounts of the bars. Ask each group to spread their bars face down, and note that players take turns selecting a bar of any color and moving their markers for the shaded amount of the bars. The first player to reach the Finish or goes beyond wins the game.

After the game discuss the concepts involved: equality, and specifically, equality involving common denominators, as all bars are being compared to the orange bars. Ask what strategies the players used. For example, some may have kept track of the types of bars that were selected to help them decide on what colors to choose. Others may have preferred to begin with the green bars since 2 out of 3 are half or more shaded and then go to the yellow bars, etc. Point out that the track on Side 2 of this mat is for bars with 10 parts, that is, for the family of tenths, fifths, and halves.

Addition Version of Small Step

In another version of the game, a player selects two bars on each turn and determines the number of steps for the total shaded amount. The player must explain his/her reasoning before moving the marker. Illustrate one turn by placing the following two transparent bars on the overhead. This turn results in 9 + 8 = 17 steps or 1 whole bar and 5 steps.

Ask players for the maximum number of steps on the mat in one turn in this game. (Answer: 24 steps for two whole bars.) After playing this game, discuss the fact that this game provides background for addition of fractions, and just as with the addition of whole numbers, addition means combining two amounts. Group Activity – Making Units: Select an arbitrary bar that is not all shaded and write its description. Then write the description of another bar for which the total shaded amount of the two bars is one whole bar. Ask a few volunteers to describe their bars. 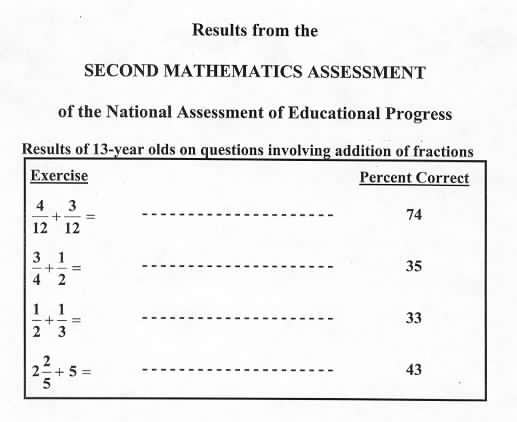Show the following result from NAEP which documents the poor performance of 13-year-olds in adding fractions. Point out that 67% missed the answer to 1/2 + 1/3 and half of the incorrect answers were 2/5. It seems likely that many students do not see addition of fractions as "combining two amounts".

Multiplication Version of Small Step

In this version of the game, each player in turn selects a bar and rolls a die. The number from the die times the number of steps from the bar determines how far the marker is moved. This game goes so fast that the winner is the first player to travel around the track twice. After playing this game, or just illustrating it to conserve time, ask for ways to determine the total number of steps for some specific bars and rolls of the die. For example, consider a red bar with 4 shaded parts and a roll of 3 on the die.

One way to determine the total number of steps is to reason that 3 times the 4 shaded parts is 12 shaded parts, and since there are 6 parts in a red whole bar, the total amount is two whole bars or 24 steps. This reasoning is recorded in the following product, and shows that this version of the game helps to provide background for the product of a whole number times a fraction:

3 x 4/6 = 12/6 = 2

Group Writing Activity Roll a die and select an arbitrary bar. Determine the number of steps on the race track in terms of whole bars and parts of a bar. Ask a few volunteers to describe their results and explain their reasoning. Discuss various methods.

The student in the following photo has just moved the marker 8 steps on the Small Step mat and is within one whole bar of completing the race. For this bar and a roll of 3 on a die, the student can move 3 x 2/3 = 6/3 = 2 whole bars or 24 steps on the mat.