Fraction Bars Philosophy & Purpose

Home

Philosophy and Purpose

The main purposes of the Fraction Bars program are to provide students with conceptual understanding of fraction notation and operations and to help them become competent in using fractions and performing operations.

The philosophy of the Fraction Bars program is based on the belief that students need non-threatening experiences with concrete models for fractions before the introduction of fraction notation and rules, and that learning should precede through the following levels: readiness - pictorial - abstract. The use of models at the readiness level and through to the abstract level reduces anxiety and provides understanding for fractions and their operations.

Each student randomly selects 10 bars and tries to place as many as possible on the mats to form equations. This provides background for writing equations.

Unlike the lengthy readiness period for whole numbers and their operations, fraction notation and their operations are often taught with little attention to models for understanding fraction concepts. Research shows that at all levels, including the college undergraduate level, fraction concepts and notation are often misunderstood.

Origin of Fraction Bars

Shortly after becoming a faculty member of the Department of Mathematics at the University of New Hampshire in 1967, I started developing activities to help prepare undergraduates for becoming elementary school teachers. The purpose of these activities was twofold: to provide a conceptual understanding of elementary mathematics; and to provide ideas that could be used to teach mathematics to elementary school students. One set of activities for learning about fractions involved strips of colored posterboard, that were later called Fraction Bars. Five samples are shown here.

After using Fraction Bars for two semesters with undergraduates, I received a call from Elsie McDonald, a grade school teacher, asking if I knew of ways to introduce fractions to her second graders. For one semester I met weekly with the second grade students and this lead to the creation of games and activities for teaching fractions.

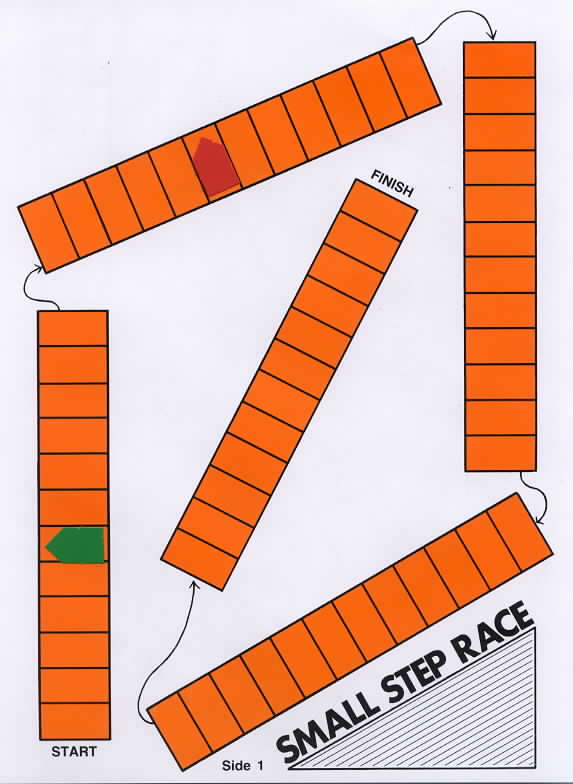
The first game that was developed was Small Step Race. This game mat has five orange bars, each divided into 12 equal parts. During the first visit to the school, the second graders played the game by randomly selecting only orange Fraction Bars. As each orange bar was selected, the amount the student's marker was moved on the race track could be determined by counting the number of shaded parts in the bar or by merely placing the bar on the mat to determine progress.

The player with the green marker moved 6 steps for a bar that was half shaded.

During my second visit to the school, the students played Small Step Race using both the orange bars and the red bars (6 equal parts per bar). They quickly learned that each shaded part of a red bar equaled 2 steps on the race mat. During subsequent visits, blue, yellow and green bars were introduced: each part of a blue bar equals 3 steps on the mat; each part of a yellow bar equals 4 steps; and each part of a green bar equals 6 steps. This introduction to Fraction Bars was nonthreatening and the students enjoyed the various versions of the game. They grew fond of whole bars (12 steps on the mat) and disliked getting zero bars.

In addition to this game, which the students played in groups of 2 to 4, there were class activities and discussions in which groups of students answered questions by using their decks of bars: "How many steps can you move on the mat for a yellow bar with one shaded part?" (Ans. 4) "What are some other bars for which you can take 4 steps on the mat?" (Ans. a red bar with 2 parts shaded or an orange bar with 4 parts shaded. Even before using fraction numerals, the background was being prepared for the part-to-whole concept of a fraction and equality and inequality of fractions.

Later on one snowy winter's day Ann Heisey, the parent of one of my son's friends, came by to pick up her son and saw the Fraction Bars. She liked the model and encouraged me to publish this method of teaching fractions. In the following months Patricia Davidson gave a workshop on Chip Trading at the University of New Hampshire and subsequently agreed to join me in developing the Fraction Bars Program.