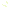Home
Suggestions and Examples
 
Research has shown that writing in mathematics helps students to organize, formulate, and clarify their ideas. There are many opportunities in the Fraction Bars program for writing about fractions. Students can describe these bars in their own words before fraction notation is introduced. Several informal descriptions are shown in the following examples.
 
 
red bar with 4 parts shaded; 6 parts with 4 parts shaded; 4 out of 6 parts shaded
 
 
blue bar with 3 parts shaded; 4 parts with 3 parts shaded; 3 out of 4 parts shaded
 
 
Readiness Level: A readiness level of activities that precedes fraction notation contains many opportunities for verbal non-symbolic descriptions. Here are a few examples.

Equality: A bar with 4 shaded parts out of 12 equals a bar with 1 shaded part out of 3.
 
Inequality: A bar with 7 shaded parts out of 12 is greater than a bar with 1 shaded part out of 2.
 
Addition: 2 parts out of 4 plus 5 parts out of 6 equals 1 whole bar and 2 parts out of 6.
 
Subtraction: 2 parts out of 3 minus 1 part out of 2 equals 1 part out of 6 .
 
Multiplication: 3 times 2 parts out of 5 equals 6 parts and since a whole bar has 5 equal parts, this product equals 1 whole bar and 1 part out of 5.
 
Division: 8 parts out of 10 divided by 1 part out of 5 equals 4. Or, the shaded amount of the 1/5 bar "fits into" the shaded amount of the 8/10 bar 4 times
 
Writing Sprints: There are also opportunities for writing about fractions in the steps beyond the readiness levels. Fifth grade teacher Mr. Schiot used to assign "writing sprints" by giving students a brief time such as 2 minutes to write about fraction operations or relations. Here are some sample questions for brief writing sessions:

1. Use a drawing to explain why 2/4 is equal to 1/2.
2. Write an explanation with diagrams to show why 2/5 is less than 4/7.
3. Sketch Fraction Bars to show that 2/3 ÷ 1/6 is equal to 4.
4. Draw a diagram to show why 1/2 times 1/3 is equal to 1/6.

.
Photo courtesy of Herb Moyer
 
Writing in Journals Some teachers have their students keep math journals. One idea is to give the students a "thought starter" that they complete. Here are a few examples:

Today our lesson was on equality of fractions and I was surprised to learn that . . .

One thing that I don't understand about fractions is . . .

Fractions are like "broken numbers" because . . .

Teaching Parents Games After the students have played one or more Fraction Bars games, an interesting assignment is to have them teach their parents and write about the results in their journals. I happened to be in Mr. Schiot's fifth grade class one day when the students were describing this experience. They were quite anxious to relate what happened and the results were interesting and at times very funny.

Student Papers: Many of the Fraction Bars games have strategies which the students discover and which can become a source for writing (see Super FRIO Strategies). Another source for writing comes from student descriptions of Fraction Bars games which they have revised or games they have created. To guide his students in writing a major paper, Mr. Schiot encouraged his students to use the following outline: (1) Experiences; (2) Topic choices; (3) Talking; (4) Thinking; (5) Research; (6) First draft; (7) Read to a friend; (8) Conference; (9) Revise and polish; (10) Rewrite; (11) Proofread; (12) Illustrate; (13) Publish; and (14) Share. The following paper describes a game that was created by Kelly, one of Mr. Schiot's students.

.


HomeHome