|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Equality (including Common Denominators) |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
Materials: Deck of bars per group and/or sheets of Blank Fraction Bars
|
|
|
|
|
|
|
|
|
One way to illustrate equality of fractions is to find bars having the same shaded amount. Place the transparent bar for 2/3 on the overhead and ask for descriptions of all the bars with the same shaded amount. Write some of the equalities. (2/3 = 4/6 . . . . 2/3 = 8/12 . . . . 4/6 = 8/12) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
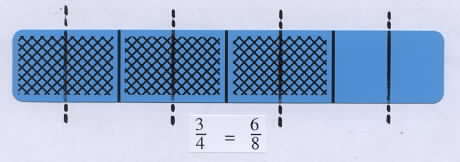
Another way to illustrate equality of fractions is to split the parts of the bar. Place a 3/4 bar on the overhead, cover it with a clear blank transparent sheet, and write the fraction 3/4 below the bar. Then by drawing on the sheet, split each of the four parts in half and write the new fraction for the bar. This shows that 3/4 is equal to 6/8.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Group Activity |
|
|
|
|
|
|
|
|
|
|
|
|
Select an arbitrary bar, write its fraction, imagine splitting each part of the bar into three equal parts (or use water-base pens to draw lines), and write the new fraction for the bar. Ask for a few volunteers to describe their results. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
Splitting each part of a 1/2 bar into three equal parts results in a bar with six parts and three shaded parts. So 1/2 = 3/6.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Discuss this method of creating equal fractions and note that splitting each part of a bar into two equal parts doubles the total number of parts and also doubles the number of shaded parts; and splitting each part of a bar into three equal parts triples the total number of parts and also triples the number of shaded parts, etc. In general, this splitting process illustrates why equal fractions are obtained by multiplying the numerator and denominator of a fraction by the same number. This is a rule that is printed in textbooks, a/b = na/nb, but it is often not illustrated. A few illustrations such as in the above activity would help to show that this rule makes sense. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Common Denominators |
|
|
|
|
|
|
|
|
|
Obtaining common denominators for two fractions can be illustrated with the bars. Place transparent bars for 2/3 and 1/5 on the overhead and ask how these bars can be split so that both have parts of the same size. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(Split each part of the 2/3 bar into 5 equal parts and split each part of the 1/5 bar into 3 equal parts.) Point out that getting the same size parts for two bars is like getting the same denominator for two fractions. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
In this game of Concentration the object is to turn over two fraction playing cards with equal fractions. The player in the foreground got lucky using the strategy of selecting green cards, the halves, since there are only three of each type of fraction on these cards. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Photo courtesy of Herb Moyer |
|
|
|
|
|