|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Multiplication Involving Fractions |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Materials: Deck of bars, a die, sheets of Blank Fraction Bars, a collection of markers for each group; and paper and pencil for each student
|
|
|
 |
|
|
|
|
|
|
The concept of multiplication involving whole numbers should be extended to products involving fractions. One way to do this is to review the meaning of multiplication of whole numbers. For example, 3 x 5 means 3 of the 5s. That is, 3 x 5 = 5 + 5 + 5 and the first number in the product tells how many times the second number occurs. This connection to multiplication of whole numbers forms the basis for understanding multiplication of fractions, as shown in the following cases.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Whole Number Times Fraction |
|
|
|
Show a bar for 2/3 and ask how the total shaded amount could be determined if there were 5 of these bars. This is like selecting a 2/3 bar and rolling a 5 on the Small Step Race mat.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Explanation: 5 of these bars will have a total of 10 parts and since each whole bar has 3 parts, 10 shaded parts is represented by 3 whole bars and 1 part out of 3. This explanation can be recorded using fractions as follows:
. . . . . . . . . . . . . . . . 5 x 2/3 = 10/3 = 3 1/3
Group Activities
a. Select an arbitrary nonzero bar, roll a die, and compute the product of the whole number times the fraction.
b. Make up a word problem that requires computing 5 x 2/3.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fraction Times Whole Number |
|
|
|
|
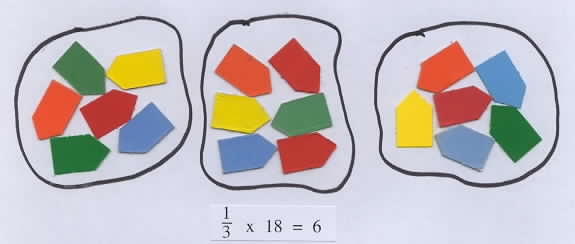
To compute a fraction times a whole number, such as 1/3 x 18, we can think; 1/3 of 18. In this case the first number still tells what to do with the second number, and 1/3 tells us to "divide the clooection into 3 equal parts and take one of them". |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Group Activities
a. Select an arbitrary collection of markers and compute 1/2 times their number. Note: If a person has an odd number of markers, one marker will need to be cut in half.
b. Make up a word problem that requires computing 1/3 x 18.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fraction Times Fraction |
|
|
|
Show a bar for 1/3, and ask what fraction would represent half of this shaded amount. Illustrate this by splitting the shaded part into 2 equal parts and double shading one of them. This double shaded part is 1/6 of a whole bar, which can be shown by comparing it to a 1/6 bar or by splitting each of the 3 parts of the 1/3 bar into two equal parts. Taking 1/2 of 1/3 is an example of multiplying by a fraction and can be recorded by the following equation: 1/2 x 1/3 = 1/6.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Group Activities:
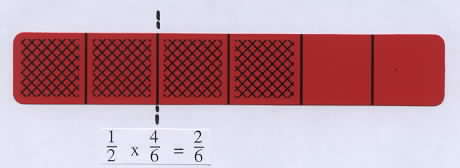
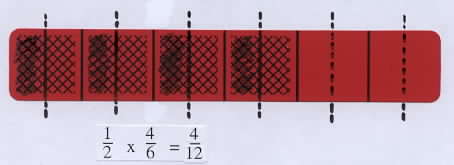
a. Select an arbitrary bar, determine 1/2 of the shaded amount, and write the resulting product. This can be done by drawing on the bars with water-base pens or shading blank bars. Discuss some of the results. For a bar with an even number of shaded parts, such as the bar for 4/6, one of the following methods might be used: take half of the shaded parts, as shown on the left below; or split one of the shaded parts in half to get 1/12 and do this for all four shaded parts, as shown below on the right. Point out that this second method leads directly to the standard algorithm for multiplying fractions:
. . . . . . . . numerator times numerator and denominator times denominator. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
 |
|
|
|
|
|
|
Take 1/2 of the total shaded part. |
|
|
|
Take 1/2 of each shaded part. |
|
|
|
|
|
b. Make up a word problem which requires computing 1/2 x 1/3.
Example: If brother has 1/3 of an apple and sister takes 1/2 of it, how much will she have?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c. For further activities involving multiplication of a fraction by a fraction use Blank Fraction Bars together with activity #5 Shading Blank Fraction Bars to Determine Products of Fractions. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Research Results |
|
|
|
|
|
|
The National Assessment of Educational Progress has found the common student belief that multiplying produces a larger number.
We can help students dispell this incorrect notion by connecting multiplication of whole numbers to multiplication of fractions. If the first number in a product is greater than 1, this number tells us how many times to add the second number. In this case multiplication produces a number bigger than the second number. (repeated addition). If the first number is a fraction less than one, then the product will be smaller than the second number because fractions less than one tell us to take part of an amount. In this case multiplication produces a number smaller than the second number.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
NAEP 4th Assessment Results |
|
|
|
|
|
Project the following NAEP result and discuss. Note that products C, D, and E all involve repeated addition and that these products involve convenient numbers. That is, products C and D are whole numbers and product E does not involve simplifying. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
In the following game of Spin and Multiply, the whole number from the spinner is multiplied by the fraction from the playing card to determine progress on the Small Step mat. Sometimes the results can be exciting for one player and discouraging for the other, such as a large number from the spinner and a card with a fraction equal to zero. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|




