|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Capture (equality, subtraction) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
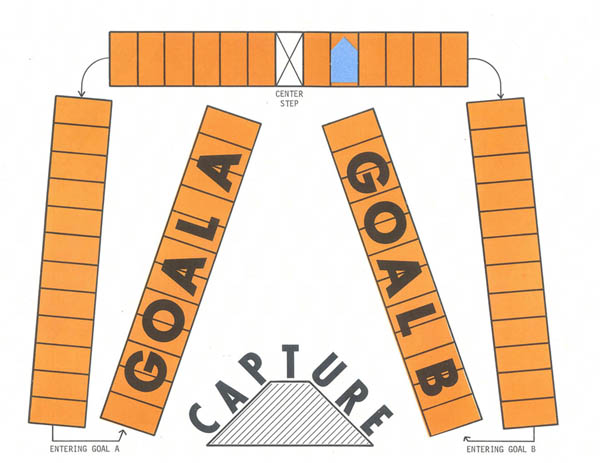
Materials: Deck of Fraction Bars, Capture mat, and marker for each pair of players |
|
 |
|
|
|
Illustrate the game Capture by placing one marker on the Center Step of the mat, and assume that Player A selects a 1/3 yellow bar and Player B selects a 1/2 green bar.
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Move the marker 4 steps toward Goal A for Player A’s turn and 6 steps toward Goal B for Player B’s turn. This results in a gain of two steps for Player B, as shown below .The game is like a ‘rope-tug". On each turn the two players each select a random bar and first one player and then the other moves their marker toward their goal. When both players have used the shaded amount of their bar for a given turn, and the marker is moved into a goal by one player but is not moved out of the goal by the other player on that turn, then the marker is captured. Theoretically the game could go on indefinitely, but it usually ends fairly quickly.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Following the game discuss the major concepts are involved: equality, inequality, and subtraction. It is interesting to watch students play this game because they will gradually discover that it is only necessary for the player with the greater shaded amount to move the marker. Students will usually see this when the two shaded amounts are equal or close to being equal. Then they may continue to play by both moving the marker on each turn before eventually seeing that the move can be completed by just one player by determining the difference in the shaded amounts of the bars. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Group Writing Activity |
|
|
|
|
|
|
|
|
|
|
Select two random nonzero bar, compare the two bars, and write a subtraction statement for the difference in the shaded amounts (larger minus smaller). Ask for a few volunteers to describe their bars and the difference. Some students may use fractions for their descriptions, but the bars and their difference can be described without using fraction notation. For example, a blue bar with 3 parts shaded minus a yellow bar with one part shaded equals an orange bar with 5 parts shaded. Illustrate a few differences for pairs of fractions with the bars. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Discuss the importance of having students write such verbal descriptions. Later they will use the briefer more convenient fraction notation, as shown in the following equation, to describe relationships and operations which they understand. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3/4 - 1/3 = 5/12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
These students are comparing bars to determine who will move the marker on the Capture mat. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Photo courtesy of Herb Moyer |
|
|

